「ビッグデータ」という言葉の普及により、ハイテク業界で最も人気が高まってきています。前回の記事では、ビッグデータ、機械学習、データマイニングの概念を簡単に紹介しました。
コンピューターに過去のデータを分析させ、未来のデータを予測させる機械学習は身近なところに広く活用されています。機械学習を専門としないエンジニアでも活用できるようになりました。今回は、機械学習を習おうとしている人向けに、最も一般的に使用される機械学習のアルゴリズムをいくつか紹介したいと思います。
1. 決定木
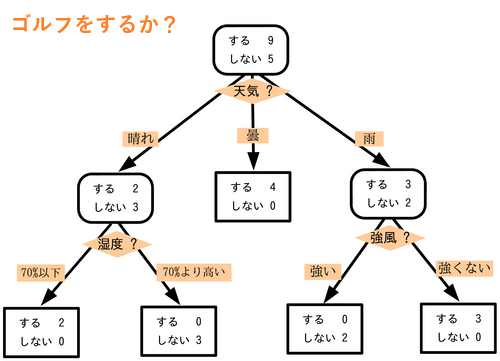
決定木は、条件分岐によってグループを分割して分類する手法です。その際にグループがなるべく同じような属性で構成されるように分割します。下の画像を見るとより理解しやすいと思います。
このように条件分岐を繰り返すことで、データはツリー状にどんどん展開され、解くべき最小単位に分割されていきます。
2.ランダムフォレスト
ランダムフォレストとは、分類や回帰に使える機械学習の手法です。決定木をたくさん作って多数決する(または平均を取る)ような手法です。ランダムフォレストは大量のデータを必要としますが、精度の高い予測/分類を行えるという特徴があります。
例を見てみましょう:
学習データ:[X1、X2、X3、… X10]があります。以下に示すように、ランダムフォレストは、バギング(bootstrap aggregatingの略です)を使って、データセットを3つのサブセットに分割し、サブセットからデータをランダムに選択して3つの決定木を作成することができます。最終出力は多数決(分類の場合)または平均値(回帰の場合)を決定します。

3.ロジスティック回帰
ロジスティック回帰は、ベルヌーイ分布に従う変数の統計的回帰モデルの一種です。予測対象の確率Pが0<P<1であれば、普通の線形モデルでは満たすことができません。 定義域が一定のレベル内にない場合、その範囲は指定された間隔を超えます。
以下はロジスティック回帰モデルと線形モデルの形です。
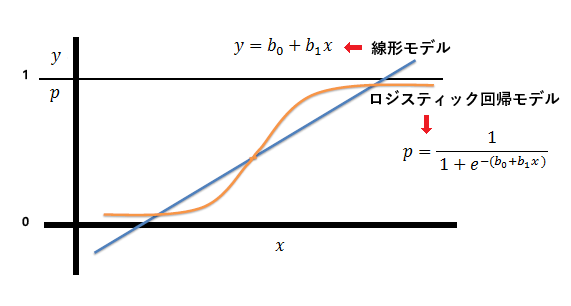
ロジスティック回帰は一般に以下のような場面で実際に使われています。
・クレジットスコアリング
・マーケティングキャンペーンの成功率の測定
・特定の製品の収益予測
・特定の日に地震が起こるか否かの予測
4.サポートベクターマシン(SVM)
サポートベクターマシンは、教師あり学習を用いるパターン認識モデルの一つで、線形入力素子を利用して2クラスのパターン識別器を構成する手法です。
SVMでは、下図のように、2つのグループ間の最も距離の離れた箇所(最大マージン)を見つけ出し、その真ん中に識別の線を引きます。
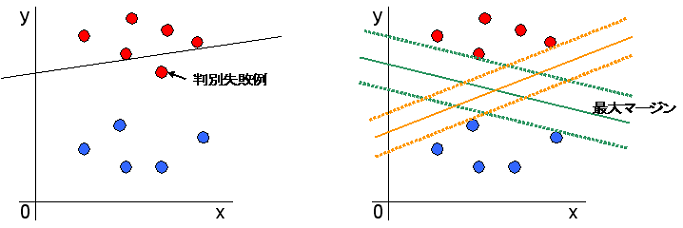
図の例では、オレンジ色の線より、緑色の線の方が両者を隔てる幅が広いため、適切な線と言えます。
適切に実装されたSVMが解決できる問題は、ディスプレイ広告、人間スプライスサイト認識、画像ベースの性別検知、大規模な画像分類などとされています。
5.ナイーブベイズ分類器
ナイーブベイズ分類器は特徴間に強い(ナイーブな)独立性を仮定した上でベイズの定理を使う、確率に基づいたアルゴリズムです。
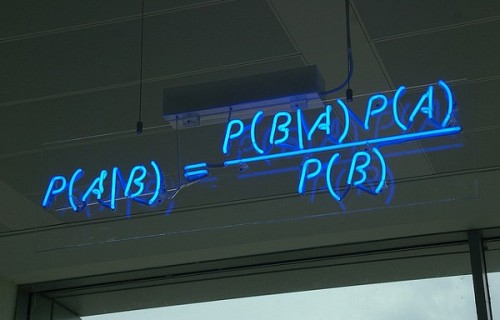
この画像はベイズの定理を表しており、P(A | B)は事後確率、P(B | A)は尤度、P(A)は分類クラスの事前確率、P(B)は予測変数の事前確率です。ナイーブベイズは主にテキスト分類などに使われ、メールのスパム/非スパム判定、テキストの肯定的/否定的な感情チェックやWebに投稿された記事のタグ付けなどに活用されます。
6.K近傍法
K近傍法は、特徴空間における最も近い訓練例に基づいた分類の手法であり、パターン認識でよく使われます。K近傍法は、機械学習アルゴリズムの中でも簡単なアルゴリズムと言われております。理由は、インスタンスの分類を、その近傍のオブジェクト群の多数決で行うことで決定するからです。
例えば下図の場合、クラス判別の流れは以下となる。
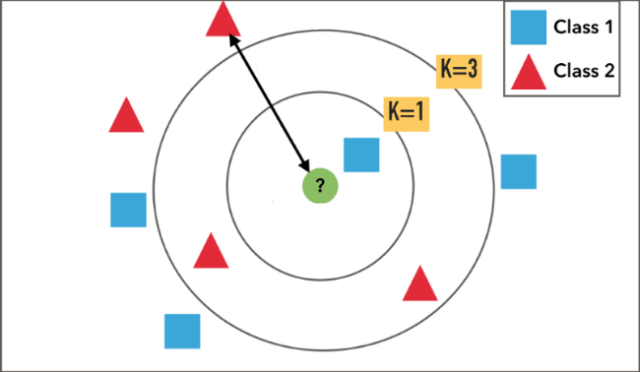
1.既知のデータ(学習データ)を赤の三角形と青の四角形としてプロットしておく。
2.Kの数を決めておく。K=1とか。
3.未知のデータとして緑の丸が得られたら、近い点から1つ取得する。
4.その1つのクラスの多数決で、属するクラスを推定。
今回は、未知の緑の丸はClass 1に属すると推定します。
※Kの数次第で結果が変わるのでご注意ください。K=3にすると、緑の丸はClass 2と判定されます。
7.K平均法
K平均法は、クラスタリングと呼ばれる、データを性質の近い分類同士でグループ分けするためのアルゴリズムのひとつです。クラスタリングの最も簡単な手法の一つであり,教師なし学習です。ここではK平均法の原理を少し説明します。
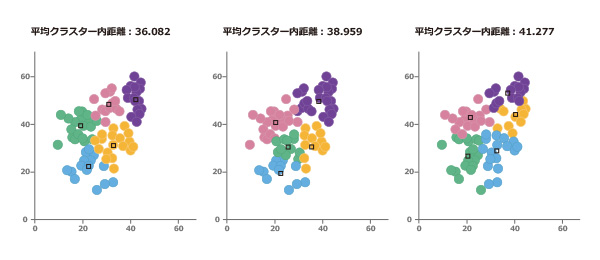
ステップ1:クラスターの「核」となるK個のサンプルを選ぶ。(ここでは5個)
ステップ2:全てのサンプルとk個の「核」の距離を測る。
ステップ3:各サンプルを最も近い「核」と同じクラスターに分割する。(この時点で全てのサンプルがk種類に分けられた)
ステップ4:K個のクラスターの重心点を求め、それを新たな核とする。(ここでは重心点の位置が移動している)
ステップ5:重心点の位置が変化したら、ステップ2に戻る。(重心が変化しなくなるまで繰り返す)
ステップ6:重心が変化しなくなったので終了する。
8.アダブースト
アダブーストはランダムよりも少し精度がいいような弱い識別機を組みわせて、強い識別機を作成しようとする機械学習モデルです。
作り方の流れは、まず、弱い識別機の適用させ、誤分類してしまったものの重みを増やし、そして、次にその重みがついたものを優先的にみて、分類する。ということを繰り返します。
下記の図を参考にするとわかりやすいです。
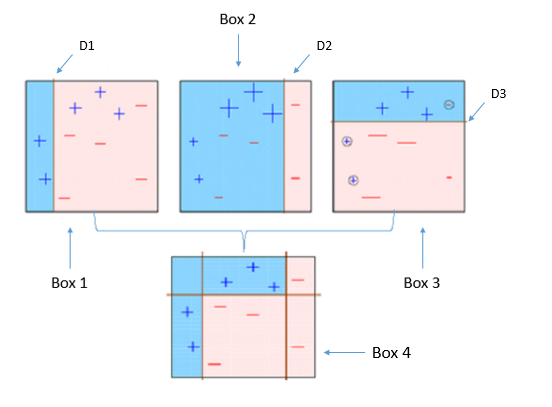
上記の図では、最初にD1で弱い識別機を使って、分類し、D2で誤分類した ‘+’1個と’-‘2個の重みを増やしています。次にその誤分類された3つを優先的に考えて、また分類しています。ここで、重みを増やすのと同時に、正確に分類された他のものの重みは減っています。さらに、D3では、D2で誤分類された’-‘3個の重みを増やすと同時に他のものの、重みは減っています。その繰り返し行った分類の重みを元に、強い識別機というものを作ります。
9.ニューラルネットワーク
ニューラルネットワークとは、人間の脳神経系のニューロンを数理モデル化したものの組み合わせのことです。
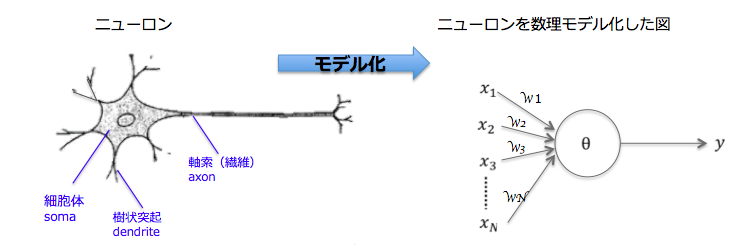
これは、ニューロンの振る舞いを簡略化したモデルです。人工のニューラルネットワークは生物学的な脳とは異なり、データの伝達方法は事前に層、接続、方向について個別に定義され、それと異なる伝達はできません。
ニューラルネットワークは、一つの層のすべてのニューロンが次の層のニューロンに接続するような一連のニューロンの層で構成されています。
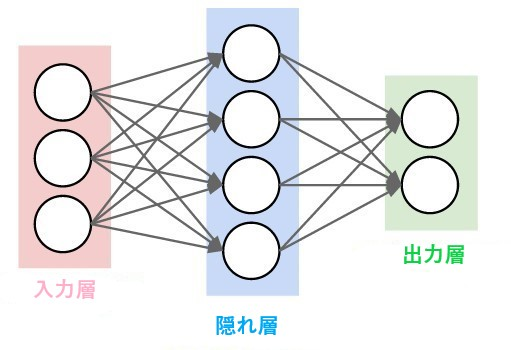
したがって上の図は、1つの隠れ層を持つ2層のニューラルネットワークです。詳しく見ると、3つの入力ニューロンと、隠れ層に2つのニューロン、2つの出力ニューロンで構成されています。
計算は次の順に行われます。左の入力層から開始し、そこから値を隠れ層に渡してから、隠れ層は出力層に値を送り最終出力となります。
10.マルコフ連鎖
マルコフ連鎖は、一連の確率変数 X1, X2, X3, … で、現在の状態が決まっていれば、過去および未来の状態は独立であるものです。
マルコフ連鎖の具体例として,以下のようなモデルを考えます(確率はかなり適当ですがマルコフ連鎖の理解には役立ちます)。
昨日以前の天気は翌日の天気に影響しない。
今日晴れ→翌日晴れる確率は 0.7,曇の確率は 0.3,雨の確率は 0
今日曇→翌日晴れる確率は 0.4,曇の確率は 0.4,雨の確率は 0.2
今日雨→翌日晴れる確率は 0.3,曇の確率は 0.3,雨の確率は 0.4
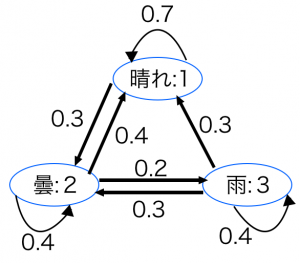
このモデルは図のように表現することができます。このような図を状態遷移図と言います。
まとめ
機械学習のスキルを持つエンジニアは企業からのニーズが高く、スキルを習得できれば大きな武器になることでしょう。アルゴリズムを完璧に理解するためには高度な数学的理解が求められますので、いろいろな勉強が必要です。今回ご紹介したのはただ浅いものですが、機械学習へ興味をお持ちになった方は是非ご参照ください。
機械学習やデータサイエンスを基礎から学ぼうとしたら、こちらの学習サイト(AIデータサイエンス特化スクール)をおすすめです。興味のある方はぜひご利用ください!




